9 tugas logis bahwa gigi hanya intelektual
Pembentukan Program Pendidikan / / December 19, 2019
1. ulang Tahun Cheryl
Misalkan beberapa Bernard dan Albert baru-baru ini bertemu dengan gadis Cheryl. Mereka ingin tahu kapan ulang tahunnya - untuk mempersiapkan hadiah. Tapi Cheryl adalah hal yang lebih kecil. Alih-alih menjawab, dia memberikan orang-orang daftar 10 tanggal kemungkinan:
| 15 Mei | 16 Mei | 19 Mei |
| 17 Jun | 18 Jun | |
| 14 Jul | 16 Jul | |
| Agustus 14 | Agustus 15 | Agustus 17 |
Bisa ditebak menemukan bahwa pria muda tidak bisa menghitung tanggal yang benar, Cheryl berbisik di telinganya, Albert panggilan hanya satu bulan kelahirannya. Dan Bernard - juga tenang - hanya nomor.
- Hmm, - kata Albert. - Aku tidak tahu kapan ulang tahun Cheryl. Tapi aku tahu bahwa Bernard tidak tahu ini.
- Ha - memenuhi Bernard. - Pada awalnya saya tidak tahu kapan ulang tahun Cheryl, tapi sekarang aku tahu itu!
- Ya, - setuju Albert. - Sekarang, saya tahu itu juga.
Dan mereka disebut di tanggal tertentu serempak. ketika Cheryl ulang tahun?
Jika Anda tidak dapat pergi untuk menemukan jawabannya, jangan khawatir. Untuk pertama kalinya pertanyaan ini diminta dalam remaja Olimpiade Matematika di Singapura
Singapura dan Asian School Math OlympiadYang terkenal dengan standar pendidikan tertinggi. Setelah salah satu presenter lokal menerbitkan layar ini teka-teki untuk Facebook, itu menjadi viralKapan hari ulang tahun Cheryl? 'The rumit matematika masalah yang memiliki orang bingung: Memecahkan itu mencoba untuk puluhan ribu pengguna Facebook, Twitter, Reddit. Tapi semua telah gagal.Kami yakin bahwa Anda akan mendapatkan. Otgadku tidak terbuka sampai setidaknya tidak mencoba.
Lihat jawabannya.
Hide.
16 Juli. Ini mengikuti dari dialog yang terjadi antara Albert dan Bernard. Ditambah proses sedikit eliminasi. Lihat.
Jika Cheryl lahir pada Mei atau Juni, jadi ulang tahunnya bisa 19 atau ke-18. Angka-angka ini ditemukan hanya dalam satu daftar waktu. Dengan demikian, Bernard, mendengar mereka, hanya bisa melihat sekitar satu bulan yang bersangkutan. Tapi Albert, sebagai berikut dari replika pertama, saya yakin Bernard, mengetahui jumlah, pasti tidak akan dapat memanggil satu bulan. Jadi, kita tidak berbicara tentang Mei atau Juni. Cheryl lahir di bulan, setiap tanggal tersebut di mana ada ganda di bulan yang berdekatan. Yang - pada bulan Juli atau Agustus.
Bernard, siapa tahu lahir, mendengar dan menganalisis replika Albert (yaitu, mencari tahu tentang Juli atau Agustus), mengatakan bahwa sekarang tahu jawaban yang benar. Dari ini berikut bahwa sejumlah Bernardo - tidak 14, karena diduplikasi, dan pada bulan Juli dan Agustus, sehingga tidak mungkin untuk menentukan tanggal yang benar. Tapi Bernard percaya diri dalam keputusannya. Jadi, jumlah yang dikenal dia tidak dua kali lipat pada bulan Juli dan Agustus. Di bawah kondisi ini mendapatkan tiga pilihan: 16 Juli, Agustus 15 dan 17 Agustus.
Pada gilirannya, Albert mendengar kata-kata Bernard (dan logis sebelum mencapai di atas tiga tanggal mungkin), menyatakan bahwa sekarang juga tahu tanggal yang benar. Kita ingat yang dikenal Albert selama satu bulan. Jika bulan ini adalah bulan Agustus, pemuda tidak dapat menentukan jumlah - pada kenyataannya, pada bulan Agustus menampilkan hanya dua. Jadi, hanya ada satu pilihan - 16 Juli.
2. putri berapa umur
Di jalan satu hari, dua mantan teman sekelas bertemu dan mengadakan dialog antara mereka.
- Hello!
- Hello!
- Bagaimana kabarmu?
- Baik. Tumbuh dua anak perempuan, doshkolnitsy lebih.
- Dan berapa umur mereka?
- Nah-di... produk dari usia mereka adalah sama dengan jumlah merpati di kaki kami.
- Informasi ini tidak cukup bagi saya!
- senior seperti ibunya.
- Sekarang aku tahu jawaban atas pertanyaan Anda!
Jadi berapa tahun anak perempuan salah satu lawan bicara?
Lihat jawabannya.
Hide.
1 dan 4 tahun. Sejak jawabannya menjadi jelas hanya setelah menerima informasi bahwa salah satu putri yang lebih tua, jadi sebelum ada ambiguitas. Pada awalnya, berdasarkan jumlah merpati, varian bahwa anak perempuan - kembar (yaitu, usia mereka adalah sama). Hal ini hanya mungkin dengan jumlah merpati adalah nomor persegi sampai dengan 7 (berusia 7 tahun - usia ketika anak-anak pergi ke sekolah, yang, berhenti menjadi anak-anak prasekolah): 1, 4, 9, 16, 25, 36, 49.
Dari kotak ini, hanya satu dapat diperoleh dengan perkalian dua nomor yang berbeda, yang masing-masing sama dengan atau kurang dari 7, 4 - (1 × 4). Dengan demikian, anak-anak perempuan 1 dan 4 tahun. Lain seluruh sementara "pre" Tidak ada alternatif.
3. Di mana mobil saya?!
Mereka mengatakan masalah ini diberikan oleh siswa kelas junior sekolah Hong Kong. Anak-anak memutuskan secara harfiah dalam hitungan detik.
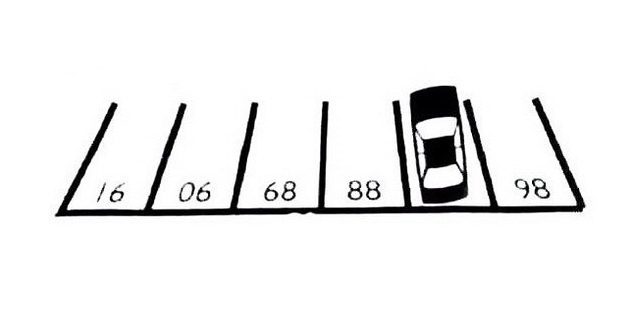
Nama jumlah ruang parkir, yang mengambil mobil.
Lihat jawabannya.
Hide.
87. Menebak, hanya melihat gambar di sisi lain. Maka angka yang Anda lihat sekarang terbalik, mengambil posisi yang tepat - 86, 87, 88, 89, 90, 91.
4. Cinta di Kleptopii
Jan dan Maria saling mencintai, berkomunikasi hanya melalui internet. Jan ingin mengirim Mary cincin pernikahan di surat - untuk menawari. Tapi di sini intinya: negara tercinta hidup di Kleptopii di mana setiap paket yang dikirimkan melalui surat, terikat untuk dicuri - jika tidak tertutup dalam sebuah kotak dengan kunci.
Pada John dan banyak istana Mary, tapi saling mengirim kunci lain, mereka tidak bisa - karena kunci juga akan dicuri. Bagaimana mengirim cincin Jan untuk itu tentu telah mendapat ke tangan Mary?
Lihat jawabannya.
Hide.
Yang harus mengirim Maria cincin dalam kotak terkunci. Tanpa kunci, tentu saja. Maria menerima parsel, harus tertanam di dalam benteng sendiri.
Kemudian Jan mengirim sebuah kotak lagi. Dia membuka sendiri kunci dan kunci re-alamat nya paket dengan kunci terkunci hanya tersisa Mary. Dan gadis itu adalah kunci untuk itu.
Kebetulan, tugas ini - bukan hanya permainan teoritis logika. Digunakan dalam ide yang - fundamentalTujuh Puzzle Anda Pikirkan Anda Tak Harus Memiliki Heard Benar Key Exchange prinsip kriptografi Protokol Diffie - Hellman. Protokol ini memungkinkan dua atau lebih pihak untuk mendapatkan kunci rahasia bersama melalui aman saluran komunikasi mendengarkan.
5. Dalam pencarian pemalsuan
kurir membawa Anda 10 tas, masing-masing dengan banyak koin. Dan semua akan baik, tetapi Anda menduga bahwa uang di salah satu tas palsu. Semua Anda tahu pasti - bahwa ini apa koin nyata berat 1 g masing-masing, dan palsu - 1,1 g Perbedaan lainnya antara uang di sana.
Untungnya, Anda memiliki skala digital yang akurat, yang menunjukkan berat hingga sepersepuluh gram. Tapi kurir terburu-buru.
Singkatnya, tidak ada, Anda hanya diberikan satu upaya untuk menggunakan beban. Seperti dalam salah satu menimbang secara akurat menghitung di mana satu tas palsu koin dan apakah ada tas seperti sama sekali?
Lihat jawabannya.
Hide.
Satu berat cukup. Hanya menempatkan pada timbangan hanya 55 koin: 1 - dari tas pertama, 2 - di kedua, 3 - di ketiga, empat - dari keempat... 10 - dari kesepuluh. Jika sejumlah besar uang akan berat 55 g - begitu palsu tidak di salah satu tas. Tapi jika berat badan akan berbeda, Anda segera akan mengerti apa nomor urut tas penuh palsu.
Pertimbangkan jika indikasi bobot akan berbeda dari referensi 0,1 - koin palsu di tas pertama, 0,2 - di kedua, 0,3 - di ketiga... 1.0 - sepersepuluh.
6. ekor kesetaraan
Dalam gelap-gelap (sekarang tidak melihat DIG, dan Anda tidak dapat menyalakan lampu), ruangan adalah meja yang 50 koin. Anda tidak melihat mereka, tetapi Anda dapat menyentuh, sandal. Dan yang paling penting, tahu persis: 40 koin awalnya terletak up elang, dan 10 - ekor.
Tugas Anda - untuk berbagi uang menjadi dua kelompok (tidak harus sama) yang masing-masing adalah jumlah yang sama koin sampai ekor.
Lihat jawabannya.
Hide.
Bagilah koin ke dalam dua kelompok: satu 40, 10 lainnya. Sekarang giliran semua uang dari kelompok kedua. Voila dapat meliputi cahaya: tugas selesai. Jangan percaya padaku - cek.
Untuk pedants matematikawan menjelaskan algoritma. Setelah pemisahan buta menjadi dua kelompok di sini adalah apa yang terjadi: ekor kiri pertama; dan kedua, masing-masing, - (10 - x) ekor (untuk total masalah 10 kondisi ekor). Sebuah elang dengan demikian - 10 - (10 - x) = x. Artinya, jumlah elang di kelompok kedua adalah jumlah ekor dalam pertama.
Lakukan langkah sederhana - menyerahkan semua koin di sekelompok kedua. Dengan demikian, semua koin-elang (potongan) adalah koin-ekor, dan jumlah mereka sama dengan jumlah ekor pada kelompok pertama.
7. Bagaimana tidak untuk menikah
Setelah pemilik toko-toko kecil di Italia berutang sejumlah besar untuk rentenir tersebut. Kemungkinan untuk membayar utang dia tidak. Tapi ada seorang putri cantik, yang telah lama mencintai pemberi pinjaman.
- Mari melakukannya, - telah menawarkan penjaga toko lintah darat. - Anda vydaosh putri saya, dan saya ingat sebagai hubungan tugas. Nah, di tangan?
Tapi gadis itu tidak mau kawin seorang pria tua dan jelek. Oleh karena itu, pemilik toko menolak. Namun, potensi anak-tangkap di ayunan suaranya dan membuat proposal baru.
- Saya tidak ingin memaksa siapa pun - kata lintah darat yang lembut. - Mari kita semua untuk memecahkan kasus ini. Lihat, Aku akan dimasukkan ke dalam tas dua batu - hitam dan putih. Dan membiarkan anak saya tanpa melihat tarikan keluar salah satu dari mereka. Jika hitam, kami telah menikah, dan aku memaafkanmu utang. Jika Putih - aku memaafkan utang begitu saja, tanpa harus menyerahkan putri Anda.
Kesepakatan itu tampak adil, dan kali ini ayah saya setuju. Rentenir membungkuk ke trek penuh dengan kerikil, cepat mengambil batu dan menempatkan mereka dalam tas. Tapi anak itu melihat hal yang mengerikan: keduanya kerikil hitam! Apapun itu ditarik keluar, ia harus menikah. Tentu saja, hal itu mungkin untuk mengekspos rentenir dalam penipuan, mengambil baik di batu yang sama. Tapi itu bisa datang ke marah dan membatalkan transaksi dengan meminta utang secara penuh.
Setelah berpikir selama beberapa detik, dia yakin mengulurkan tangannya untuk kantong. Dan saya melakukan sesuatu yang disimpan ayahnya dari utang, dan itu sendiri - kebutuhan untuk menikah. Keadilan rentenir bahkan mengakui tindakannya. Apa sebenarnya yang dia lakukan?
Lihat jawabannya.
Hide.
Dia menarik sebuah batu, dan tanpa harus menunjukkan siapa pun, jika tidak sengaja menjatuhkannya di trek. Batu kemudian dicampur dengan sisa kerikil.
- Oh, aku sangat canggung! - tangan tergenggam putri pemilik toko. - Tapi itu tidak ada. Setelah semua, kita dapat melihat dalam tas. Jika ada batu putih, jadi aku menarik hitam. Dan sebaliknya.
Tentu saja, ketika semua tampak dalam tas, ada ditemukan sebuah batu hitam. Bahkan rentenir Saya harus setuju: itu berarti bahwa gadis itu ditarik putih. Dan jika demikian - pernikahan tidak akan dan harus memaafkan utang.
8. Anda telah bingung kode ...
Anda menutup koper pada kunci digital dengan nomor kode tiga digit dan sengaja dilupakan. tapi ingatan Ia menawarkan tips berikut:
- 682 - kode ini adalah salah satu nomor yang benar dan di tempatnya;
- 614 - salah satu nomor benar, tetapi tidak harus di tempat;
- 206 - benar dua digit, tetapi keduanya tidak di tempat;
- 738 - semua omong kosong, tidak ada memukul;
- 870 - Salah satu tokoh adalah benar, tetapi tidak pada tempatnya.
Informasi ini cukup untuk menemukan kode yang tepat. Apa itu?
Lihat jawabannya.
Hide.
042.
Berikut ujung keempat, mencoret semua kombinasi nomor 7, 3 dan 8 - mereka dalam kode yang diinginkan pasti tidak. Kami mencari tahu dari petunjuk pertama bahwa tempatnya adalah 6 atau 2. Tetapi jika itu adalah 6, itu bukan kondisi Petunjuk kedua di mana 6 berdiri di awal. Jadi, angka terakhir dari kode - 2. Sebuah 6 tidak ada dalam cipher.
Dari petunjuk ketiga kami menyimpulkan bahwa nomor yang tepat dari kode - 2 dan 0. Dalam hal ini 2 adalah di bagian bawah. Ini berarti bahwa 0 - di tanah. Dengan demikian, kita menjadi sadar akan digit pertama dan ketiga dari kode: 0... 2.
Apakah dibandingkan dengan Petunjuk kedua. Gambar 6 dangkal sebelumnya. Unit tidak cocok: diketahui bahwa tidak pada tempatnya, tetapi semua lokasi yang mungkin untuk itu - pertama dan terakhir - sudah diduduki. Dengan demikian, angka yang benar adalah hanya 4. Dan pindah ke tengah kode yang dihasilkan - 042.
9. Bagaimana membagi kue
Dan akhirnya, sedikit manis. Apakah Anda punya torteYang harus dibagi dengan jumlah tamu - 8 buah. Satu-satunya masalah adalah bahwa hal itu perlu dilakukan, setelah membuat hanya tiga luka. Ke kanan?
Lihat jawabannya.
Hide.
Membuat dua luka melintang - seperti jika Anda ingin membagi kue menjadi empat bagian yang sama. Sebuah sayatan babatan ketiga tidak vertikal tetapi horizontal di sepanjang pemisah memperlakukan.

lihat juga🔎🤓✌️
- 10 tugas pada logika dan kecerdasan
- 4 menjelaskan logika utama dari undang-undang tentang contoh sederhana
- 5 alat yang efektif untuk pengembangan kreativitas
- Memecahkan teka-teki 3 trik dan mencari tahu seberapa pintar Anda
- 10 tugas sulit untuk logika uji dan kecerdasan



